不同公共卫生干预对健康生命、发病率和预期寿命的影响

文 | Paula Diehr, Ann Derleth, Liming Cai and Anne B Newman

翻译 | 崔中砥

研究背景：

公共卫生的首要重点是促进健康和疾病预防，但是不同最具效率的预防方法的应用环境却比较模糊。其关键点在于要了解哪些策略能给社会带来最大的利益，这样有限的资源才能得到有效的利用。健康的社会和行为决定因素有许多概念框架，如医学研究所或埃文斯和斯托达特提出的框架。关于健康干预有个人层面的理论，如健康信念模型和跨理论模型。也有社区或团体层面的理论，包括生态观点，社区组织，和社会营销。然而，这些理论都没有直接针对不同人群的预防和治疗方向。也就是说，这些理论不能够有效地证明让健康的人保持健康、让病人恢复健康、防止病人死亡或防止健康的人死亡。

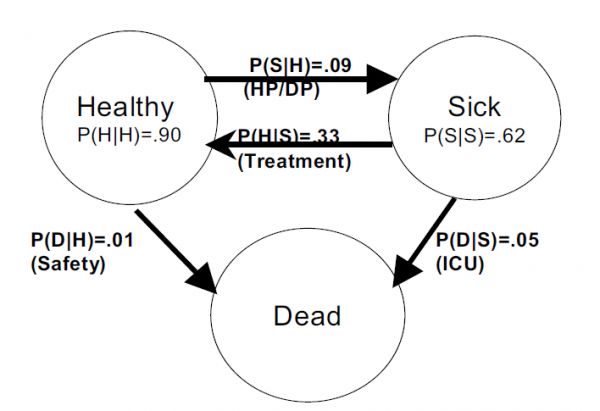
图1.65岁在一年内的三个不同的健康状态，P(A|B)是65岁时处于B状态的人在66岁时处于A状态的概率。例如，P(S|H)是健康的65岁老人在66岁时生病的概率。括号中的数量代表将影响相关转移概率的一般干预，如图所示。HP/DP是健康促进和疾病预防，它影响健康人患病的概率。治疗使病人更健康。重症监护室降低了病人死亡的可能性。安全干预减少了健康人死亡的机会。

图1表示“公众”属于三种状态之一：健康、生病或(随着时间的推移)死亡。箭头表示人可以改变状态。图中的转化概率为65岁人群一年内在不同健康状况下的转化概率。例如，使用标准概率表示法，P(S|H) = 9%表示如果65岁的人今年健康，他明年生病的概率是9%。在图1中，健康促进和疾病预防可以被认为主要是降低健康人患病的概率。然而，降低健康或患病人员死亡的概率(P(D|H)或P(D|S))或增加患病人员恢复健康的概率(P(H|S))也将改善公众的健康。这些方法在实现公共卫生目标方面有何不同？

图1可以被认为是一个有三种状态的系统，健康、生病和死亡。系统在任何时候的状态完全由其初始条件(基线时健康和患病人数)和向不同状态转变的概率来定义。因此，公共卫生干预试图通过改变初始条件、改变转变概率或两者兼而有之来改善健康。

初始条件可以通过在基线时将一些人从患病状态转变到健康状态来改善(以下称为一次性干预)。干预也可以旨在改变每个年龄层的转变概率。通过健康促进或疾病预防项目(HP/DP)，这种干预可能会降低健康人患病的概率P(S|H)。改进的治疗方法和获得治疗的途径可以增加病人恢复健康的可能性P(H|S)。改善重症监护室(ICU)护理等干预措施可能会降低病人死亡的概率P(D|S)。最后，改善交通、枪支或工作场所安全的干预措施可以降低健康人的死亡率P(D|H)。人们也可以结合干预措施，如HP/DP+ 一次性干预，或HP/DP+ICU。这种干预措施可能对寿命或寿命年数、健康寿命年数(YHL)、发病率或患病寿命年数以及医疗支出产生不同的影响。

表1

干预类型在表1中进行了正式定义，表1提供了每种干预类型的代数、文本和助记符描述。一次性干预将所有病人移至健康状态，仅在基线时一次。考虑到不太有效的干预，我们将一次性干预定义为仅在基线时移动100*λ%健康患者的干预，其中参数λ的值小于或等于1。在每个年龄提高转变概率的四种干预被代数地描述为参数α的函数，α是相关年龄特定转变概率的“提高”量。例如，HP/DP是将P(S|H)乘以(1-α)的干预；为了达到10%的改善，α = 0.10，P(S|H)乘以0.9，因此健康人在每个年龄患病的概率降低了10%。

干预类型的名称不是指真正的干预，而是被选择来帮助读者记住干预的主要特征。考虑一个向人群提供抗生素的公共卫生干预。如果每次仅有部分(可能是全部)病人使用抗生素，目标是使100*λ%的病人立即健康，这将是一次强度用λ来衡量的干预。如果每年向一部分病人提供抗生素，目标是将一年后健康的病人比例增加(1+α)倍，这就是用强度α来衡量的治疗。每年给病人样本注射抗生素以降低他们的死亡概率将是一种重症监护室式的干预。并且每年对健康人的样本施用的抗生素将是HP/DP或安全型干预，这取决于主要目标是预防疾病还是预防死亡。因此，抗生素计划将根据目标、时机和主要预期效果进行不同的分类。更多讨论部分给出了详细的例子。

本文的目的是比较不同类型的干预策略对生命年数、健康生命年数和患病生命年数(YOL、YHL、YSL)以及医疗费用的影响。我们假设HP/DP干预表现良好，因为预防是公共卫生的首选策略。然而，在有些情况下，预防可能不是最好的办法，因为干预的有效性取决于干预的性质和力度、目标人群的初始健康状况和年龄，以及社会对患病寿命的重视。

研究方法

健康状况和转化概率

我们把“健康”定义为身体极好、非常好或很好，“生病”指健康状况一般或较差。从三个大的数据集中计算各州之间的年龄特异性转换概率。多状态寿命表由转换概率计算。根据初始条件（基线健康和患病人数）和过渡概率，寿命表提供了从基线到100岁的未来健康寿命年数（在健康状态下度过的年数）的估计值。国家对0岁和65岁健康或患病人群比例的估计来自全国健康访谈调查。按年龄和健康状况分列的医疗支出数据是根据2002年收集的MEPS数据，使用MEPSnet软件估算的。这些数据被用来估计未来每项干预的医疗支出。

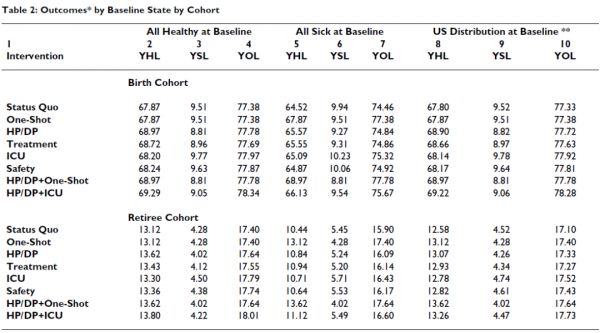
表2

我们检查了表2中列出的干预类型的表现。“现状”干预没有改变，是比较基础的。“一次性干预”是一种干预措施，仅在基线时将100%的患者转移到健康类别（在本文的大部分内容中，将λ设置为1）。我们还定义了四种假设性干预措施，每种干预措施都会影响图1中的过渡概率。我们计算了每一个跃迁概率“提高”100*α%的效果。这种改善的定义是将P（H|S）乘以1+(以增加恢复的概率），或者将P（S|H）、P（D|H）或P（D|S）乘以1-(以减少生病或死亡的概率）。我们还评估了表2所示的两种综合干预措施，并将每种干预措施与“现状”干预措施进行了比较。

添加额外YHL和YSL的价值

考虑两种假设的干预措施，A和B。干预措施A增加4年的健康寿命，不增加患病寿命，而B增加3年的健康生命年数(YHL)和2年的患病生命年数(YSL)。哪种干预更好?答案取决于额外增加一个YHL或YSL对社会的价值。价值可以用美元来衡量(可能是基于生产力的损失或病人医疗支出的增加)，或者其他一些方式。假设我们知道额外的YHL对社会价值100“单位”，额外的YSL价值为0;那么干预A会更受青睐，因为它提供了400单位的价值，而干预b提供了300单位的价值。或者，如果一个YSL值50，两种干预将是相等的，因为它们都提供了400单位的价值。如果YSL值100,YHL和YSL之间将没有区别，干预B将是首选。我们不知道绝对价值的值(甚至不知道它应该被测量的单位)，但我们可以有效地考虑YSL和YHL的相对价值。设值为附加YSL值与YHL值之比。在上述三种情况下，t = 0/100 = 0, t = 50/100 = 0.5, t = 100/100 = 1.0。

最好的干预将为社会提供最增值的投入。我们假设未来生命年的价值是K*(YHL +β* YSL)调整后的年，其中，β是一个小于或等于1的数字，K是一个可以被忽略而不丧失一般性的常数。如果β = 1，未来价值为YHL+1*YSL = YOL;社会对人的健康或疾病状态漠不关心，并将寻求最大限度地延长预期寿命。如果β= 0, future worth =YHL +0*YSL=YHL;社会对生病和死亡的国家漠不关心，而最大限度地延长健康寿命的干预将提供最有价值的价值。消极的价值观暗示疾病是一种比死亡更糟糕的状态。我们检查了在-0.25到1.0之间的范围。对于每一对干预措施，我们计算了其中一种干预措施比另一种干预措施更具成本效益的干预成本，如下所述。

分析

我们首先评估了每种干预措施的效果，采用的方法是:β=1.0，α=0.10。对于HP/DP+一次性干预，我们将所有患者移至基线时的健康状态，并通过提升α来改良P(S|H)。对HP/DP+ICU患者，可通过提升α来提升P(S|H)和P(D|S)。使用Stata中实现的多状态生命表软件，我们估计了基线规模为100,000的队列的YOL、YHL和YSL。研究对象包括出生队列(0 - 100岁)和退休队列(65 - 100岁)。我们还估计了平均终身医疗支出，即预计在每个年龄处于每个健康状态的人数乘以该状态和年龄的平均医疗支出，再加起来除以100000。

规范比较

干预的比较要求我们标准化输入或输出。例如，当按每个质量调整生命年的成本比较干预措施时，成本是投入，QALY是产出。在这里，我们将使用社会价值增量(价值调整后的生命年数的改善)作为产出，并以两种方式解释投入。我们首先检查固定α下的产出量。因为one shot不是一个α的函数，我们还需要测试能产生固定输出的α的大小，定义为与one shot干预相同的输出。下面将对此进行更详细的解释。

研究结果

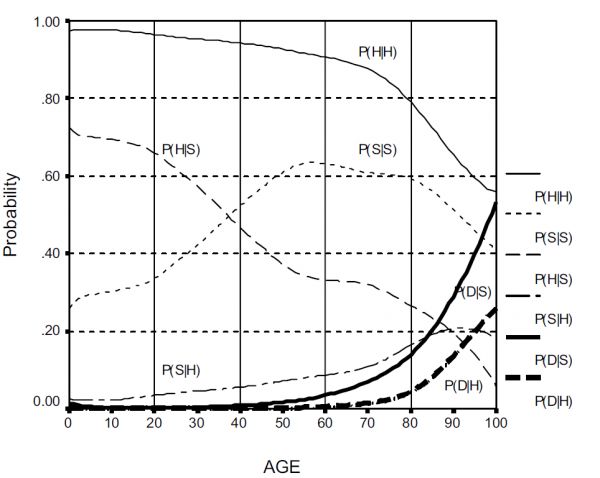
图2

图2显示了从0岁到100岁的转移概率。这些数据来自三个大型纵向数据集，在其他地方详细列出。例如，最上面的线显示了X轴上这个年龄的健康的人在一年后仍然健康的概率(P(H|H))。最低的线是生病或死亡的概率。40岁以下的概率相当有利，但40岁以后，保持或恢复健康的概率下降，患病或死亡的概率上升。提高概率的干预措施将使P(H|S)线提高10%，或使三个底线降低10%。

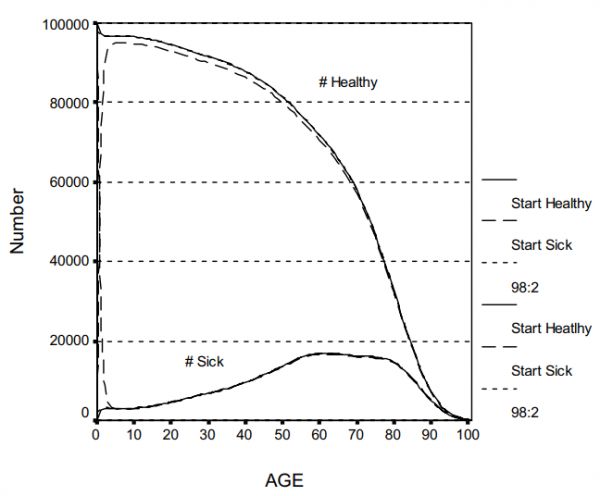
图3

图3显示了出生队列中每个年龄预计健康或患病的人数。(没有显示死亡人数)。实线代表100000人的出生队列，每个人出生时都是健康的;上面一行是长期健康的人数下面实线是生病的人数。虚线代表一个队列，每个人在出生时都生病了。一次性干预改变了最初健康或生病的比例。值得注意的是，即使在“出生时全部患病”的队列中，大多数人在几年后仍是健康的，因为P(H|S)在较年轻的年龄较高(见图2)。重要的是，直到80岁左右，患病人数相对于健康人数较少。这将对各种干预措施的有效性产生影响。

两条健康曲线下的区域是健康寿命的预期年数(YHL)，两个队列之间的差异主要是因为零岁附近的差异。表2中标有“现状”的一行(解释如下)表明，如果每个人出生时健康，YHL是67.87年；如果每个人出生时生病，则是64.52年。“患病”曲线下的区域是患病年限或发病率。第三对(虚线)代表健康和患病的人数，如果98%的人口出生时健康，类似于国家的估计。在图3中，这些线实际上与“出生时都健康”的线没有区别。YHL为67.8年。

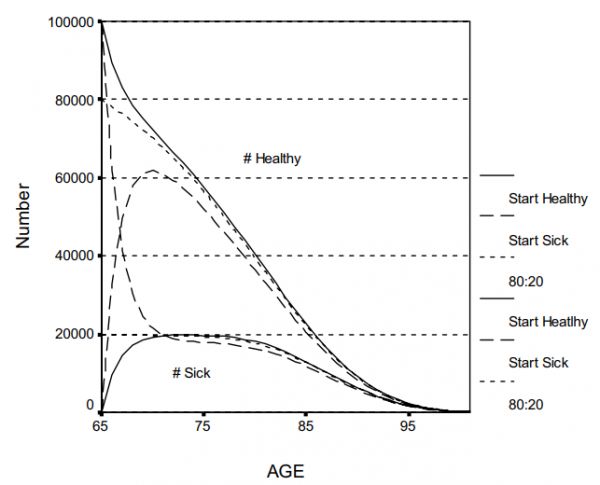
图4

图4显示了相同的信息，但针对的是退休人员群体。和以前一样，当所有人在65岁时都健康时，两条实线是健康(上线)和生病(下线)的数字。两条虚线是65岁时所有人都生病时健康和生病的人数。两条虚线反映了80%的人健康，20%的人在65岁时患病和健康的人数，类似于全国的估计。请注意，初始条件(65岁时，所有患病者对所有健康者对80%健康者)比图3中的条件更重要。所有初始条件下，健康人的数量最终会变得相似，但需要的时间比图3中的长。很明显，三条顶部曲线下的区域是不同的。如果65岁时所有人都健康，YHL估计为13.12年；如果所有人都生病，则为10.44年；如果80%的人健康，则为12.58年。

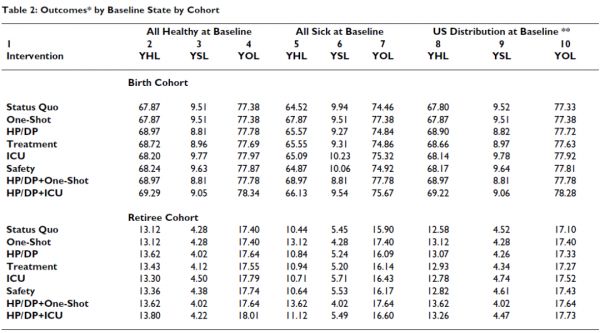
表2

表2按队列显示了每项干预措施的估计健康寿命年数、患病寿命年数和寿命年数，这取决于队列在基线时是全部健康(第2-4列)还是全部患病(第5-7列)。例如，第一行显示，在现状下，出生队列中出生时健康的人平均健康年数为67.87年，患病年数为9.51年，合计为77.38年(预期寿命)。接下来显示的是基线时病人的数值，不太理想(例如，只有74.46 YOL)。在第8-10栏中，基线时健康和患病的百分比被设置为国家值:出生队列的初始健康百分比为98%，患病百分比为2%，退休队列的健康百分比为80%，患病百分比为20%。例如，对于出生队列，第8列是0. 98*(第2列)加上0. 02*(第5列)。

YHL、YSL、YOL和医疗支出的增量变化

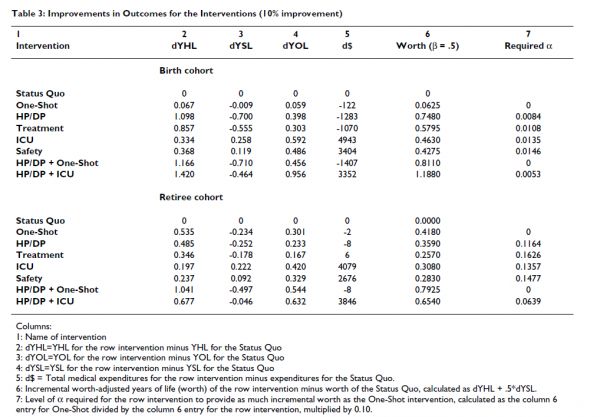
表3

表3的第2、3和4列与表2的最后三列相同，只是从每一行中减去了现状值。例如，根据定义，现状干预的dYHL(YHL的差异)为0。一次性干预在出生队列中实现了0.067年的额外健康寿命，这是表3第二行的条目。一次性干预还能减少0.009年的疾病寿命或发病率，增加0.059年的存活率。在退休人群中，一次性干预的效果更大。第5栏显示了干预造成的未来医疗支出的估计差异，单位为美元。所有的干预措施都改善了YHL和YOL(dYHL和dYOL总是正态的)，尽管这种改善通常不是很大。安全性和重症监护室干预增加了发病率和医疗费用，而其他干预降低了发病率和医疗费用。HP/DP +重症监护室降低了YSL，但增加了医疗费用。表3第2–5栏中的条目是针对α = .10计算的。然而，我们发现YHL、YSL和YOL的变化量通过|α| < 3的原点近似为α的线性函数(除了不特别依赖于α的单次注射和HP/DP +单次注射)。这种简化后来用于将标准配置扩展到其他α值。

干预的相对效果

干预措施对YOL、YHL和YSL的影响是不同的。我们假设干预对社会的增量值是K*(dYHL+β* dYSL)，其中K是一个可以忽略的常数，β是额外的YSL的相对值。首先，假设β = 0.5(额外YSL对社会的价值是额外YHL的一半)。表3第6列显示了每次干预的价值调整年增量，计算方法为dYHL+.5*dYSL。在出生队列中，两种联合干预提供了最大的价值，其次是HP/DP。退休人员的结果相似，除了一次性干预是最好的简单干预。

对社会的价值也可以用β的其他值来计算。例如，如果β = 0，价值就是dYHL，如果β = 1，价值就是dYOL。如果β值较低，降低YSL的干预措施更有价值；如果β值较高，则有利于提高YSL的干预措施。在出生队列中，如果β <0.798，则在所有单次干预中，HP/DP产生的价值最大，而重症监护病房对较高的β值最有效(计算未显示)。在退休人群中，β值< 0.741时，单次干预最有价值，β值较高时，重症监护病房干预较好。β < 0.606时，HP/DP优于ICU。因此，“最佳”干预很大程度上取决于β，即额外的YSL对社会的相对价值。

尽管第6栏允许我们比较所有干预措施的价值，这些干预措施都通过相同的因素得到了改善，α= 0.10，但一次性干预措施不是α的函数，因此不能与其他干预措施进行公平比较。为了提高可比性，第7栏显示了每次干预产生与一次性干预相同的价值调整年数所需的α值。例如，在表3的第6列中，对于退休人员，一次性的价值为0.4180，而HP/DP系统的价值仅为0.3590。要将HP/DP增加到一次性水平，我们必须将其值乘以0.4180/. 3590 = 1.164。因为增量价值被发现是通过原点的α的线性函数，将实现这种变化的α是1.164 * 10 = . 1164，其被列在第7栏中。在出生队列中，一次性干预相当于大约0.01的α，而在退休人员队列中，它相当于0.1到0.2之间的α。第7列中较低的值是优选的，因为它们表明需要较小剂量的行干预来等效于一次性干预干预。在这两个队列中，HP/DP是修改概率的最佳单次干预，而HP/DP + ICU是最佳的整体干预，即以最小的转变概率(α的最小值)实现指定的价值。

第7栏显示了初始条件与美国人口相同时所需的α，β = 0.5。更一般地说，如果π是基线健康的比例，

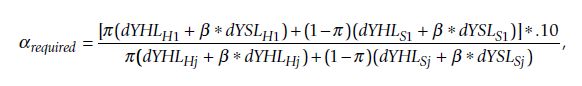
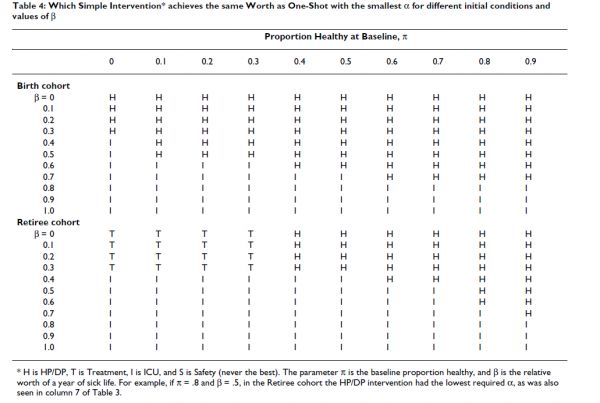
表4

其中dYHLHj表示干预引起的YHL变化，如果基线时每个人都健康，dYHLSj是基线时每个人都生病的变化，dYHLH1和dYHLS1是指一次性干预。该方程用于计算π和β的不同组合所需的α。表4显示了对于不同的π和β值，哪种简单的干预具有最低的所需α。对于出生队列，β < 0.4时，HP/DP最佳，β > 0.7时，ICU最佳，β在0.4和0.7之间时，HP/DP的π值较高时，首选ICU。对于退休人员群组，当β和π都较低时，治疗干预是优选的；也就是说，当最初的人口少于40%健康并且额外的YSL的相对价值较低时。β负值的首选干预措施与β = 0的干预措施相同，因此未单独显示。因此，表4显示，尽管在标准配置(π= 0.98或0.80，β= 0.5)下，HP/DP是优选的，但HP/DP并不总是最佳干预。对于不同的π或β值，重症监护室或治疗干预可能更可取。安全干预从来都不是最好的。表4对α和λ的所有值都是正确的，但不允许对联合干预进行评估。

另一个重要的考虑因素是实施和维护干预措施的成本。这需要指定干预的成本，以将转移概率提高100*α%(或使100*λ%的患者在基线时健康的成本)。我们表明，在某些假设下，如果一项干预措施的成本比率低于其所需α比率的倒数，则相对于另一项干预措施而言，该项干预措施具有成本效益。由于我们没有关于这些假设干预的成本的信息，对成本效益的进一步讨论仅限于讨论部分的例子。

讨论

这篇论文对文献作出了几项贡献。我们将人口概念化为具有三种(或更多)健康状态的系统。因为改变一个系统的唯一方法是改变初始条件或转变概率，所有的公共卫生干预都必须做出一个或多个这样的改变。这使我们能够对干预的类型进行分类，并以系统的方式进行比较。我们在计算中加入了β，即额外一年患病寿命的相对价值，并发现它在决定各种干预措施的相对效果方面具有影响力。通过将所有干预的输出标准化为单次干预，我们获得了不同干预的公平比较。最后，我们发现YHL、YSL和YOL的改进量是通过原点(对于|α| <0.3)的α的线性函数，这允许我们仅在少数情况下计算多状态寿命表，但将结果扩展到许多其他情况。

其他地方已经使用多状态生命表方法来估计改变转移概率、降低某些疾病或死亡原因的流行率或实现健康人2000年目标对死亡率和发病率[14-23]和医疗支出[24]的影响。该文献通常只涉及老年人(65岁或以上)，并未具体涉及可能实现此类改变的干预类型。

干预措施的特点

图2和图3显示，在这个国家，40岁以下人口的转移概率和初始条件都没有多少改善的空间。更有效的做法是针对中年人和老年人的健康，或年轻人中患病和患病或死亡概率较高的人群。所有干预措施都改善了YHL和约略水平，但旨在提高约略水平的干预措施也增加了发病率和医疗支出。表4显示了哪些类型的干预最有效，以及这个结论在多大程度上取决于π和β。

一次性干预相当于用实线代替图3中的虚线(使所有病人在基线时健康)。图3中最上面的实线和虚线之间的区域(乘以最初患病的出生队列的比例)是与一次性干预相关的附加YHL。显然，一次性干预对YHL的影响是短期的，如果基线时患病人数很少，这种影响就很小。因此，一次性在退休人群中表现更好(见图4)。通过将表3中的单次注射值减半，可以获得仅使一半患者在基线时(λ= 0.5)健康的效果。

HP/DP、治疗和一次性干预通过保持或使更多人健康而发挥作用，从而直接改善YHL和YSL。它们间接改善了YOL，因为健康人的死亡率较低。重症监护室的干预使病人免于死亡，从而直接增加了约尔和YSL，并间接增加了YHL，因为从死亡中获救的人以后可能会变得健康。安全干预直接增加了约尔和YHL，但也有些令人惊讶地增加了YSL，因为通过干预挽救的人活得足够长，可以积累YSL，而不是英年早逝。这些考虑的净效果是，前三项干预措施减少了医疗支出，而后两项增加了医疗支出。

两种联合干预的效果不同。HP/DP +一次性(退休人员群组中为0.7925)的价值略高于HP/DP和一次性(分别为0.3590+0.4180 = 0.7770)的价值之和。这种明显的协同作用可能会发生，因为这两种干预作用于分布的不同部分，单次注射最初增加了健康人的数量，以使HP/DP干预保持健康。HP/DP+重症监护室干预措施提供的价值略低于其组成部分的总和，这可能是因为HP/DP系统干预措施保持了人们的健康，使得重症监护室干预措施能够挽救更少的患者免于死亡。HP/DP+重症监护室增加了医疗支出，尽管它降低了YSL，显然是因为它使YOL发生了相对较大的变化，而YSL的下降相对较小。在发送、安全和重症监护室干预中增加一次性干预是很容易评估的。在表2和表3中，我们仅显示了幽门螺杆菌/聚合酶链反应+重症监护室，因为它优于其他组合(β= 0.5)。结合不同的干预措施将需要额外的生命表计算。

至少在美国，有可能改进转移概率和初始条件的估计，在美国，许多基于公众人群的纵向数据集可以确定感兴趣的亚人群的死亡。我们不知道β的任何来源，β是额外患病一年对社会的相对价值。需要这一信息是因为最佳干预的选择对β敏感。有证据表明β < 1，因为我们投资于不威胁生命的健康问题的治疗。最近关于协助自杀和从持续植物人状态中取消生命支持的公开讨论表明β > 0。如表4所示，通常对预防项目的公共卫生强调隐含假设出生队列中的β < .798，退休队列中的β< . 606；否则，公共卫生将强调防止病人死亡(重症监护室)，当β值较大时，重症监护室提供最有价值的调整寿命。我们显示了β= 0 . 5的结果，这是一个任意选择。有趣的是，国家健康统计中心用于计算健康寿命的方法(与此处报道的方法不同)与老年人的β值约为0.5一致。这方面需要进一步研究。

结论

虽然大量的研究已经考虑了队列的死亡率和残疾模式，我们的论文可能是第一个提出整个年龄范围内的转变概率，并检查特定类型的干预对健康寿命的影响。关于不同的干预措施如何改善公众健康，已经获得了一些见解。健康促进和疾病预防策略在大多数情况下表现良好，但重症监护室和治疗有时更好。安全干预将由通过和执行法律来实施，而不是直接干预健康和患病的人。相对于其他干预措施而言，它可能具有成本效益，尽管它从未在表4中被选中。β的重要性表明，是时候在全国范围内讨论通过增加发病率来提高存活率的干预措施对社会的价值了。同时在美国，任何年龄的患病人数都很少，大部分都归功于当今的公共卫生战略。

参考资料：

Diehr P , Derleth A , Cai L , et al. The effect of different public health interventions on longevity, morbidity, and years of healthy life[J]. BMC Public Health, 2007, 7(1):52.

声明：MEWS矩阵所刊载内容之知识产权为MEWS矩阵及相关权利人专属所有或持有。未经许可，禁止进行转载、摘编、复制及建立镜像等任何使用。

相关知识

营养干预 守护全生命周期健康
《“十四五”国民健康规划》发布 人均预期寿命提高1岁左右
预期寿命与健康预期寿命差距持续扩大 国药赛诺根黑科技瑞拓龄成新希望
公共卫生与预防医学
公共卫生的意义和作用
公共卫生
最影响寿命的25个生活习惯
生活中影响寿命的14个因素
全生命周期健康管理，公立医院应对慢性疾病的策略
我国老年人长寿不健康问题突出，健康预期寿命低

网址: 不同公共卫生干预对健康生命、发病率和预期寿命的影响 https://www.trfsz.com/newsview407732.html